Graphical-Belief in Action Graphical-Belief in Action This example is a emergency Low Presure Coolant Injection (LPCI) system analyzed by Martz and Waller [1990]. In the case of a loss of coolant accident, the two motor operated valves (MOVs) should open and the four pumps should add extra coolant (water) to the reactor. All six of these components are protected by Check Valves (CVs). The reactor will successfully respond to the accident as long as at least one of the four pumps in delivering water to the system.
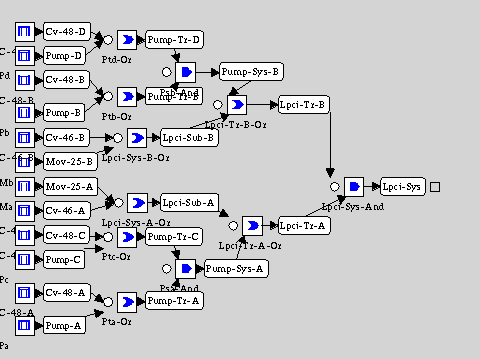
Figure 1. Graphical Model for Low Pressure Coolant Injection System.
Figure~1 shows the graphical model corresponding to this system. The nodes (oval shaped boxes) in the graph represent the states of components and subsystems in the LPCI. The square boxes are rules which define the probability distribution of the output variable given the input variables. Note that we can derive these probability distributions in many ways, either from logical rules (for example, and-gates and or-gates), directly from tables, or from another graphical model.
This is a rather simple model: all of the variables are binary and there are no loops in the graph. Graphical-Belief can analyze more complex models, but this simple example can still illustrate many of its features.
Using the data from Martz and Waller [1990], the risk of a failure of the Loss of Coolant System during an accident is 0.000004.
But "What is the overall risk of system failure?" is not the most interesting question we can ask. Graphical-Belief can answer the following kinds of questions:
Diagnosis and Importance Analysis. Find out
which components are most likely to cause a system failure.
Sensitivity Analysis. Explore the
implication of critical assumptions on the system failure rate
estimates. This topic also shows how the object oriented model
construction procedure simplifies the analysis.
Parameters and Data.
Graphical-Belief can represent complex dependencies
among probabilities using a parameter network. This example explores
how this simplifies the analysis of this model.
Model Construction. Explore the
implication of loops in the graphical model. This example also shows
how the model construction features work.
Valuations.
Graphical-Belief can use many representations of
uncertainty, including probability and belief functions this example
explores a few.
Evidence and Explanation.
Graphical-Belief contains some powerful test
selection capabilities based on the idea of weight of evidence.
This example explores a few.
Back to overview of Graphical-Belief.
View a list
of Graphical-Belief in publications and downloadable technical
reports.
The Graphical-Belief user
interface is implemented in Garnet.
Get more
information about obtaining Graphical-Belief (and why
it is not generally available).
get
the home page for Russell Almond , author
of Graphical-Belief.
Click
here to get to the home page for Insightful (the company that StatSci
has eventually evolved into).